จากความพยายามที่หาหนทางนำเอาคณิตศาสตร์มาแทนรูปทรงเรขาคณิต โดยเริ่มจากในระนาบ จึงมีการกำหนดระนาบเป็นแกนสมมุติ x, y ซึ่งแทนระนาบใด ๆ

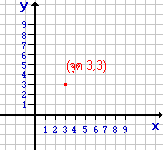
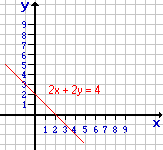
เมื่อจุดอยู่บนระนาบจึงแทนด้วยคู่ลำดับ เช่น จุด  3 , 3   และทางเดินของจุดก่อให้เกิดเป็นเส้น   เส้นตรงที่ลากผ่านจุดสองจุดบนระนาบ จึงเขียนแทนด้วยสมการทางเดินของจุด เช่น 2x + 2y = 4 เขียนเส้นทางเดินของเส้นตรงนี้ได้

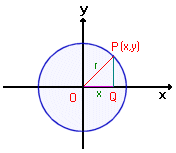            ถ้าเขียนรูปวงกลมลงบนระนาบ โดยอาศัยแกนพิกัดฉาก และให้จุดศูนย์กลางของวงกลมอยู่ที่คู่ลำดับ x , y เป็น  0 , 0 ดังรูป

            ทางเดินของจุด P(x,y)   เมื่อให้ระยะรัศมี  r  คงที่เสมอจะได้เส้นส่วนโค้งของวงกลม จากสมการของพีธากอรัสทำให้เราได้

             ซึ่งก็หมายถึงการแทนวงกลมลงบนระนาบที่มีรัศมี r และจุดศูนย์กลางอยู่ที่ (0,0) เราเขียนสมการทางเดินของจุดได้
 

             ยามค่ำคืนถ้าได้มีโอกาสสังเกตบนฟากฟ้าจะพบเห็นดาวที่สุกสว่างมีแสงเจิดจ้า ซึ่งได้แก่ดาวเคราะห์ และหากสังเกตต่อเนื่องไปหลาย ๆ วัน และอาจถึงหลายเดือนจะพบเห็นการเคลื่อนที่ผ่านกลุ่มดาวฤกษ์

             ในทางดาราศาสตร์ พบว่าทางเดินของดาวเคราะห์ต่าง ๆ และโลกโคจรรอบดวงอาทิตย์เป็นวงรี ในยุคแรกคอเปอร์นิคัส (corpernicus) เสนอทฤษฎีการโคจรของดาวเคราะห์เป็นรูปวงกลม แต่ต่อมาพบว่าไม่ถูกต้อง ในปี 1600 เคปเลอร์ (Kepler) ได้เริ่มศึกษารายละเอียดการโคจรของดาวเคราะห์ เคปเลอร์ได้ทำการบันทึกการเปลี่ยนแปลงของตำแหน่งดาวอังคารบนฟากฟ้า จนในปี 1609 ก็สามารถพิสูจน์ให้เห็นว่า ดาวอังคารเคลื่อนที่รอบดวงอาทิตย์เป็นวงรี หลังจากนั้นก็พิสูจน์ได้ว่าดวงจันทร์ และดาวบริวารต่าง ๆ หมุนเป็นรูปวงรี

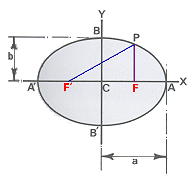            วงรี เป็นเส้นโค้งที่มีลักษณะใกล้เคียงกับวงกลม แต่มีจุดคงที่สองจุดเรียกว่า จุดโฟกัส เส้นโค้งที่เกิดจากการเคลื่อนที่ของจุด ซึ่งลากมาจากจุดโฟกัสจะทำให้ผลบวกของเส้นทั้งสองนี้คงที่เสมอ
 

            หากลากเส้นผ่านระหว่างโฟกัสทั้งสอง จะตัดวงรีที่ A และ A' ความยาวนี้มีค่าเท่ากับ 2a เรียก แกนยาวของวงรี และเส้นที่ลากผ่านจุด C ไปตามแกน Y พบกับส่วนโค้งวงรีที่ B และ B' ซึ่งมีความยาว 2b เรียกว่า แกนสั้นของวงรี สมการของรูปวงรีเมื่อเขียนในรูปสมการจะได้

            เทคโนโลยีการสื่อสารดาวเทียมประกอบด้วยจานรับสัญญาณ ตัวจานรับสัญญาณมีผิวโค้ง เพื่อรับสัญญาณที่ส่งตรงมาจากดาวเทียม และสะท้อนรวมกันที่จุดรับสัญญาณ เพื่อให้มีสัญญาณที่แรงขึ้น

            หรือเมื่อเราใช้ไฟฉายส่องเดินทาง สังเกตว่ามีกระจกสะท้อนแสงเพื่อรวมลำแสงให้พุ่งเป็นลำตรง โดยหลักการตามกฎการสะท้อนของแสง มุมตกกระทบย่อมเท่ากับมุมสะท้อน จุดที่รวมกันบนผิวระนาบโค้งนี้เรียกว่าจุดโฟกัส ผิวโค้งที่ทำให้มุมตกกระทบและสะท้อนมารวมกันที่จุดโฟกัส เรียกว่า ผิวโค้งพาราโบลา สมการของเส้นโค้งพาราโบลาเขียนได้ดังนี้

             และถ้ามีจุดคงที่หรือจุดโฟกัสสองจุดเช่นเดียวกับวงรี ถ้าให้จุด ๆ หนึ่งเคลื่อนที่ไป โดยกำหนดให้ผลต่างระหว่างจุดที่เคลื่อนที่และจุดคงที่ทั้งสองมีค่าคงที่ เราจะได้เส้นโค้งที่เรียกว่า ไฮเปอร์โบลา และจะมีเส้นโค้งนี้สองเส้นที่ไม่ต่อกัน

            การศึกษาเส้นทางเดินของจุด ทำให้เคปเลอร์ทราบวิถีการโคจรของดาวเคราะห์ และต่อมานิวตันเข้าใจถึงหลักการของแรงโน้มถ่วง และทราบถึงผลของการเคลื่อนที่ที่มีต่อแรงโน้มถ่วง นอกจากนี้ฮัลเลย์ซึ่งเป็นนักดาราศาสตร์ที่มีชื่อเสียงโด่งดังก็สามารถใช้หลักการ การเคลื่อนที่เป็นรูปวงรี และพาราโบลา และแรงโน้มถ่วงของดวงดาวต่าง ๆ ทำให้อธิบายปรากฎการณ์การเดินทางของดาวหาง และสามารถทำนายดาวหางว่าจะกลับมาให้เห็นอีกครั้งเมื่อไร
 

            การศึกษา เส้นโค้งที่กล่าวมาแล้วคือ วงกลม วงรี พาราโบลา และไฮเปอร์โบลา มีมานานแล้ว ตั้งแต่ยุคสมัยอียิปต์โบราณ ทั้งนี้เส้นโค้งเหล่านี้เกิดจากการตัดรูปกรวยที่มีฐานเป็นวงกลมด้วยพื้นราบในลักษณะต่าง ๆ

            ถ้าตัดด้านพื้นราบขนานกับฐาน ก็จะได้วงกลม ถ้าติดเอียงทำมุมก็จะได้รูปวงรี เมื่อพื้นราบเอียงจนขนานกับเส้นที่ลากจากยอดมาฐาน ก็จะได้รูปพาลาโบลา ถ้าใช้กรวยสองกรวยต่อจุดยอดกัน แล้วติดพื้นราบซึ่งตั้งฉากกับฐานกรวยจะได้รูปไฮเปอร์โบลา

            เส้นโค้งและผิวโค้งทางคณิตศาสตร์ยังมีอีกมาก และเป็นศาสตร์ที่สามารถนำมาใช้ในการออกแบบผลิตภัณฑ์ต่าง ๆ ได้มากมาย ลองค้นหาจากเอกสารต่าง ๆ ดูว่า เส้นโค้งทางคณิตศาสตร์ที่น่าสนใจเหล่านี้มีลักษณะอย่างไร cycloid, cardioid Ephicycloid Hypocycloid spiral ฯลฯ

            ประโยชน์ของเส้นโค้งหรือผิวโค้งจึงมีมากมายและเกี่ยวข้องกับชีวิตประจำวันอย่างมาก เช่น ขณะขับรถไปในท้องถนน ถ้าวิศวกรออกแบบถนนให้มีส่วนโค้งของผิวถนนขณะขึ้นสะพาน และลงระนาบพอดี ผู้ขับขี่ยวดยานจะไม่รู้สึกกระเพื่อม