การหาคำตอบของปัญหาการโปรแกรมเชิงเส้น
วิธีกราฟ
การแก้ปัญหาการโปรแกรมเชิงเส้นด้วยวิธีกราฟเหมาะที่จะใช้ในกรณีที่ตัวแปรของปัญหาไม่เกิน 3 ตัวแปร แต่ที่ใช้มากได้แก่ปัญหา 2 ตัวแปร โดยมีวิธีการ
- นำชุดเงื่อนไขบังคับไปเขียนกราฟ
- เลือกพื้นที่ให้สมจริงกับเงื่อนไขบังคับ
- หาจุดยอดและพิกัดของจุดยอดของพื้นที่สมจริงกับชุดเงื่อนไขบังคับ
- สร้างตารางหาค่าเป้าหมายตามจุดยอด
- เลือกค่าเป้าหมายที่เหมาะสม (optimum)
เราจะได้ค่าพิกัดของจุดยอดที่ตรงกับค่าเป้าหมายที่เหมาะสมเป็นคำตอบของปัญหา
จากตัวอย่างต่อไปนี้.....
| ตัวแปร | : X1 , X2  0 |
(1) |
| เงื่อนไขบังคับ | : 6X1 + 6X2  420 |
| : 3X1 +6X2 300 |
(2) |
| : 4X1 +2X2 240 |
| เป้าหมาย | : P = 300X1 + 200X2 = Max |
(3) |
ก่อนที่จะนำอสมการไปเขียนกราฟ เราจะต้องหาจุดผ่านของกราฟเสียก่อนโดยจะต้องเปลี่ยน อสมการเป็น สมการแล้วเขียนกราฟ
| 6X1+6X2 = 420 |
| 3X1+6X2 = 300 |
| 4X1+2X2 = 240 |
เขียนกราฟและเลือกพื้นที่ที่สมจริงกับอสมการของชุดเงื่อนไขบังคับได้ ดังนี้
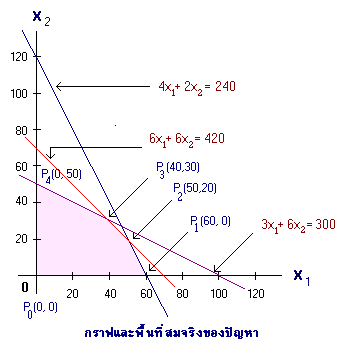พิกัดของจุดยอดต่างๆเรารู้ได้เฉพาะจุดP0, P1 และ P4 ส่วนจุด P2 และ P3 เราต้องแก้สมการคู่ที่ก่อให้เกิดจุดตัดของจุดยอดนั้นๆก้จะได้พิกัดของจุด P2(50,20) และ P3(40,30)
ต่อไปสร้างตารางหาค่าเป้าหมายตามจุดยอดจาก P = 300X1 + 200X2 ได้ดังนี้
 | P0 | P1 | P2 | P3 | P4 |
|---|
| X1 | 0 | 60 | 50 | 40 | 0 |
| X2 | 0 | 0 | 20 | 30 | 50 |
| P | 0 | 18,000 | 19,000 = Max | 18,000 | 10,000 |
จากตาราง P มีค่าสูงสุดที่จุด P2 คือ Pmax = 19,000 บาท
ดังนั้นบริษัทอุตสาหกรรมจะต้องผลิตผลิตภัณฑ์ทั้งสองชนิด ดังนี้
| ผลิตภัณฑ์ชนิดที่ 1จำนวน 50 หน่วย |
| ผลิตภัณฑ์ชนิดที่ 2 จำนวน 20 หน่วย |
| กำไรสูงสุดเท่ากับ 19,000 บาท |
ดูอีกตัวอย่างหนึ่ง........
| ตัวแปร | : X1 , X2 0 |
(1) |
| เงื่อนไขบังคับ | : 6X1 + 2X2 12 |
| : 2X1 + 2X2 8 |
(2) |
| : 4X1 + 12X2 24 |
| เป้าหมาย | : C = 40,000X1 + 32,000X2 = Min |
(3) |
จากชุดอสมการของเงื่อนไขบังคับ เราหาจุดผ่านของกราฟในรูปของสมการ ดังนี้
| 6X1 + 2X2 = 12 |
| 2X1 + 2X2 = 8 |
| 4X1 + 12X2 = 24 |
เขียนกราฟและเลือกพื้นที่ที่สมจริงได้ดังรูป
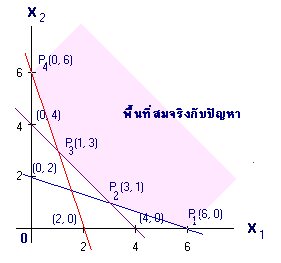เราได้จุดยอดพร้อมด้วยพิกัดเป็น P1 (6,2), P2(3,1), P3(1,3)และ P4(0,6) นำจุดยอดไปทดสอบหาค่าต่ำสุดและเป้าหมายของอสมการ C = 40,000X1 + 32,000X2 ได้ดังตารางต่อไปนี้
| P1 | P2 | P3 | P4 |
|---|
| X1 | 6 | 3 | 1 | 0 |
| X2 | 0 | 1 | 3 | 6 |
| C | 240,000 | 152,000 | 136,000 = Min | 192,000 |
จากตารางค่าต่ำสุดที่จุด P3 คือ C min = 136,000 บาท
ดังนั้น บริษัทจะต้องจัดการผลิตแร่ดังนี้
| เหมือง A ทำงาน 1 วัน /สัปดาห์ |
| เหมือง B ทำงาน 3 วัน/ สัปดาห์ |
| ต้นทุนการผลิตต่ำสุดเป็น 136,000 บาท / สัปดาห์ |
ที่มา : เอกสารคณิตศาสตร์ กข. Brand's Summer Camp ปี 1998