| ตัวอย่างการแก้ปัญหาด้วยวิธีซิมเพล็กซ์
|
|
| maximize
| 6 x1
| +
| 4 x2
| +
| 0 x3
| +
| 0 x4
| =
| z
|
|
เงื่อนไข
| 2 x1
| +
| 3 x2
| +
| x3
|
|
| =
| 100
|
|
|
| 4 x1
| +
| 2 x2
|
|
| +
| x4
| =
| 120
|
|
| เมื่อ
| x1  >0x2>0
|
| |
เขียนสมการเหล่านี้ใหม่
| maximize
| z
เขื่อนไข
| z
| -
| 6 x1
| -
| 4 x2
|
|
|
|
| =
| 0
|
| ....... R1
|
|
|
|
|
| 2 x1
| +
| 3 x2
| +
| x3
|
|
| =
| 100
|
| ....... R2
|
|
|
|
|
| 4 x1
| +
| 2 x2
|
|
| +
| x4
| =
| 120
|
| ....... R3
|
| | |
การคิดรอบที่ 1 พิจารณา
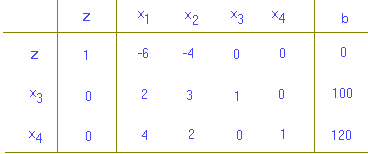
พิจารณาแถวแรก z ค่าสัมประสิทธ์ที่มีค่าน้อยสุด คือ -6 จึงเลือก x1 เป็นตัวแปรขาเข้า พิจารณา 100/2 > 120/4 ดังนั้นจึงเลือก x4 เป็นแถวขาออก
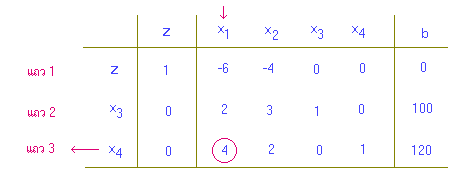
เพื่อการปรับค่า ให้ x1 ในแถวที่ 1 และแถวที่ 2 เป็น 0 และให้แถวที่ 3 เป็น 1 โดยการแทนแถวที่ 3 ด้วย แถวที่ 3 หารด้วย 4 แถวที่ 1 ด้วย 6 คูณแถวที่ 3 + แถวที่ 1 และแถวที่ 2 ด้วย -2 คูณแถวที่ 3 + แถวที่ 2 ได้ผลลัพธ์
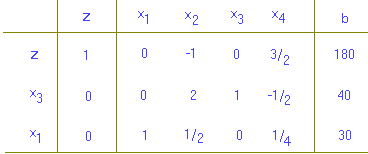
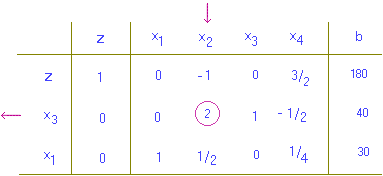
พิจารณาแถวที่ 1 เพื่อเริ่มการคำนวณรอบต่อไป เห็นว่าค่า -1 ในแถวที่ 1 เป็นค่าน้อยสุด จึงแลือก x2 เป็นตัวแปรขาเข้า ได้
|
| ดังนั้นจึงเลือกแถวที่ 2 หรือ x3 เป็นตัวแปรขาออก
| |
ในการปรับค่าให้ x2 ในแถวที่ 2 เป็น 1 แถวที่ 2 หาได้จากการหารด้วย 2 แถวที่ 1 ทำให้ x2 มีค่าเป็น 0 โดยการนำ แถวที่ 2 มาบวก และแถวที่ 3 ทำได้ด้วยการนำเอา -1/2 มาคูณแถวที่ 2 แล้วบวกกับแถวที่ 3 ผลลัพธ์ที่ได้
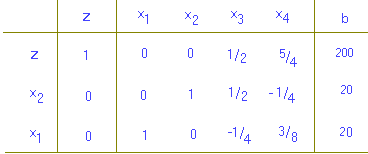
คำตอบที่ได้คือ x1 มีค่า 20 x2 มีค่า 20 x3 และ x4 มีค่าเป็น 0 z ได้ 200
พิจารณาจากตัวอย่างการทำ Minimize
| Minimize
| z
| =
| x1
| +
| x2
| -
| 4 x3
|
อสมการเงื่อนไข
| x1
| +
| x2
| +
| 2x3
| <
| 9
| x1
| +
| x2
| -
| x3
| <
| 2
| -x1
| +
| x2
| +
| x3
| >
| 4
| x1, x2 ,x3
| >
| 0
| | | |
ในกรณีนี้เราแปลงให้อยู่ในรูปสมการได้
| Minimize
| x1
| +
| x2
| -
| 4x3
| +
| 0x4
| +
| 0x5
| +
| 0x6
|
|
เงื่อนไข
| x1
| +
| x2
| +
| 2x3
| +
| x4
| | | |
| = 9
|
| x1
| +
| x2
| -
| x3
| |
| +
| x5
| |
| = 2
|
| - x1
| +
| x2
| +
| x3
| | | |
| +
| x6
| = 4
|
| x1 , x2 , x3
| >
| 0
| | | | |
เมื่อเขียนในรูปสมการที่ใช้สำหรับตารางซิมเพล็กซ์
|
| Minimize
| (z)
| =
| -
| Max
| (-z)
| | | |
|
| |
| =
| -
| Max
| ( - x1
| -
| x2
| +
| 4 x3)
|
เงื่อนไข
|
| - z
| + x1
| +
| x2
| -
| 4x3
|
|
| |
| x1
| +
| x2
| +
| 2x3
| +
| x4
| | | |
| = 9
| |
| x1
| +
| x2
| -
| x3
| |
| +
| x5
| |
| = 2
| |
| - x1
| +
| x2
| +
| x3
| | | |
| +
| x6
| = 4
| | | |
นำมาเขียนลงตารางสำหรับการคำนวณแบบซิมเพล็กซ์
การคำนวณรอบที่ 1
ได้ x3 เป็นตัวแปรขาเข้า และ x6 เป็นตัวแปรขาออก
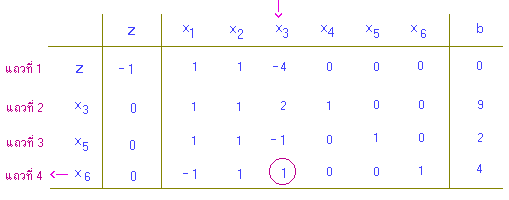
การคำนวณ