วิธีพิจารณา
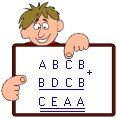
(1) A และ B และ C ไม่เป็นศูนย์ เพราะเป็นตัวเลขในหลักพัน
(2) เนื่องจาก B ในหลักหน่วยของตัวตั้งและตัวบวกรวมกันได้ A จะได้ A เป็นจำนวนคู่ (จำนวนเต็มใด ๆ รวมกับตัวเองเป็นจำนวนคู่)
(3) เนื่องจาก C ในหลักสิบของตัวตั้งและตัวบวกรวมกันแล้วได้จำนวนคู่ (คือ A ) แสดงว่าไม่มีตัวทดจาก B + B นั่นคือ B + B ต้องน้อยกว่า 10 ซึ่งเป็นไปไม่ได้เมื่อ B ต้องไม่เกิน 4
ถ้า B ในหลักหน่วยเป็น 4 จะได้ A ในหลักหน่วยเป็น 8 ซึ่งจะเห็นว่าผลบวกของ A และ B ในหลักพันจะเป็น 12 ซึ่งเป็นไปไม่ได้ (เพราะ C ต้องน้อยกว่า 10) ดังนั้น B เป็น 4 ไม่ได้
ถ้า B ในหลักหน่วยเป็น 3 จะได้ A ในหลักหน่วยเป็น 6 ซึ่งทำให้ C ในหลักพันเท่ากับ 9 ดังนั้นผลบวกของ C กับ C ในหลักสิบเป็น 18 ซึ่งจะทำให้ A เป็น 8 ขัดแย้งกับที่หาได้ว่า A = 6 ดังนั้น B เป็น 3 ไม่ได้
ถ้า B ในหลักหน่วยเป็น 1 จะได้ A ในหลักหน่วยเป็น 2 ซึ่งทำให้ผลบวกของ C กับ C ในหลักสิบเป็น 12 (คือ A = 2) ดังนั้น C =6 แต่ผลบวกของ A กับ B ในหลักพัน (คือ C ) เท่ากับ 1 + 2 = 3 ซึ่งขัดแย้งกัน ดังนั้น B เป็น 1 ไม่ได้
| | | |
 นั่นคือ
นั่นคือ
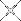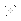 นั่นคือ
นั่นคือ